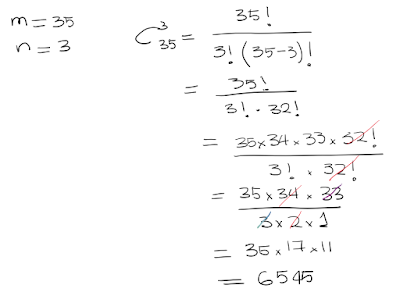COMBINACIONES

Para comenzar con este contenido, es imprescindible que comprendas la diferencia entre PERMUTACIÓN y COMBINACIÓN. Para ello te invito a que realices el siguiente Test.

Ahora si: ¡Empecemos! 

Una combinación es un arreglo de elementos seleccionados de un conjunto. Sin importar el orden en que se tomen los elementos.

Este arreglo puede hacerse:

1. Repitiendo los elementos Pensemos en que  vamos a pedir un helado de 3 bolas, y hay 5 sabores para escoger: banana, chocolate, limón, fresa y vainilla. Podemos elegir 3 sabores diferentes e inclusive podemos repetir el sabor que más nos guste ¿quién no ha repetido un sabor de helado? DEFINICIÓN La combinación con repetición de m elementos, tomados de n en n (m ≥ n), son los distintos grupos posibles que pueden hacerse con los m elementos de forma que: No entran todos los elementos. No importa el orden.  Si se repiten los elementos. Ejemplo. En una bodega hay 5 tipos   diferentes de botellas  ¿de cuántas maneras se pueden elegir 4 de ellas? m= 5 y n=4 R/De los 5 tipos de botella,  se pueden escoger de 70 formas, 4 de ellas.

2. Sin repetir los elementos Pensemos que de las 16 bolas de billar  pool, tomaré las bolas 1, 2 y 3.  No me importa el orden en que  las tome, siempre serán las  bolas marcadas con los números  1, 2 y 3.  Si me importara el orden de los números, inmediatamente esto se me convertiría en una PERMUTACIÓN. Es decir, que si me importara el orden, tendría 6 maneras diferentes de sacar las  3 bolas. Así: 123 132 312 213 231 321 Pero en una COMBINACIÓN, este no es el caso y  no importa el orden en que se hayan tomado. Siempre serán las 3 bolas numeradas con el 1, 2 y 3. DEFINICIÓN Se llama combinación de m elementos, tomados de n en n (m ≥ n), a todas las agrupaciones posibles que pueden  hacerse con los m elementos de forma que: No entran todos los elementos. No importa el orden. No se repiten los elementos. puede ser: Ejemplo. En una clase de 35 estudiantes  se quiere elegir un comité  formado por 3 de ellos  ¿cuántos comités podrían resultar? R/De los 35 estudiantes,  pueden resultar 6545 comités  formados por 3 personas.

Combinaciones: Practica y aprende:

“AYÚDANOS A SALVAR EL PLANETA" 

TEN CONCIENCIA AMBIENTAL

PAPERLESS