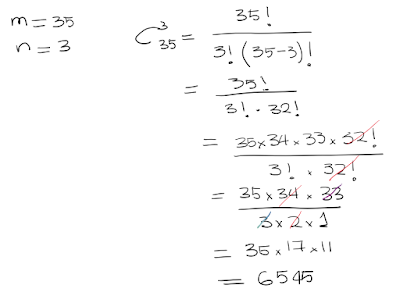Números primos del 1 al 1000

Read More

Amor en Familia

Read More

Test de Combinaciones

Read More

COMBINACIONES

Para comenzar con este contenido, es imprescindible que comprendas la diferencia entre PERMUTACIÓN y COMBINACIÓN. Para ello te invito a que realices el siguiente Test.

Ahora si: ¡Empecemos! 

Una combinación es un arreglo de elementos seleccionados de un conjunto. Sin importar el orden en que se tomen los elementos.

Este arreglo puede hacerse:

1. Repitiendo los elementos Pensemos en que  vamos a pedir un helado de 3 bolas, y hay 5 sabores para escoger: banana, chocolate, limón, fresa y vainilla. Podemos elegir 3 sabores diferentes e inclusive podemos repetir el sabor que más nos guste ¿quién no ha repetido un sabor de helado? DEFINICIÓN La combinación con repetición de m elementos, tomados de n en n (m ≥ n), son los distintos grupos posibles que pueden hacerse con los m elementos de forma que: No entran todos los elementos. No importa el orden.  Si se repiten los elementos. Ejemplo. En una bodega hay 5 tipos   diferentes de botellas  ¿de cuántas maneras se pueden elegir 4 de ellas? m= 5 y n=4 R/De los 5 tipos de botella,  se pueden escoger de 70 formas, 4 de ellas.

2. Sin repetir los elementos Pensemos que de las 16 bolas de billar  pool, tomaré las bolas 1, 2 y 3.  No me importa el orden en que  las tome, siempre serán las  bolas marcadas con los números  1, 2 y 3.  Si me importara el orden de los números, inmediatamente esto se me convertiría en una PERMUTACIÓN. Es decir, que si me importara el orden, tendría 6 maneras diferentes de sacar las  3 bolas. Así: 123 132 312 213 231 321 Pero en una COMBINACIÓN, este no es el caso y  no importa el orden en que se hayan tomado. Siempre serán las 3 bolas numeradas con el 1, 2 y 3. DEFINICIÓN Se llama combinación de m elementos, tomados de n en n (m ≥ n), a todas las agrupaciones posibles que pueden  hacerse con los m elementos de forma que: No entran todos los elementos. No importa el orden. No se repiten los elementos. puede ser: Ejemplo. En una clase de 35 estudiantes  se quiere elegir un comité  formado por 3 de ellos  ¿cuántos comités podrían resultar? R/De los 35 estudiantes,  pueden resultar 6545 comités  formados por 3 personas.

Read More

Test de Permutaciones y Combinaciones. ¿El orden importa?

Read More

Métodos para Recolectar Datos

Read More

Variables Estadísticas

VARIABLES ESTADÍSTICAS

¡Hola!

En esta ocasión, aprenderemos el elemento más importante de una investigación estadística.

Generalmente, cuando deseamos saber más acerca de un fenómeno o proceso, recojemos datos para después analizar la información.  

Este proceso de recolección de datos se llama observación.

Datos

Los datos son una serie de hechos, representados en forma de números, palabras, medidas, observaciones o simplemente descripciones de cosas.  Estos pueden ser de tipo Cualitativo o Cuantitativo. Los de tipo cualitativo ofrecen información descriptiva de algo, mientras los cuantitativos ofrecen cantidades numéricas.

Los datos recolectados serán registrados bajo una variable, sobre la cual se desea hacer el estudio. Esta variable, representará las propiedades o características de un evento, un objeto o persona, y  como su nombre lo indica puede tomar diferentes valores o cantidades.  Por ejemplo, puedo estudiar la preferencia del chocolate de acuerdo a la edad y el sexo de un grupo de personas. 

 

Recuerda que si en los datos encontrados, se encuentra el mismo valor, este dato ya no será una variable sino una constante.

Por ejemplo, si realizo una investigación estadística canina, puedo definir varias variables de estudio: ALTURA, PESO, COLOR DEL PELO, LARGO DEL PELO, FORMA DE LA CABEZA y al recolectar los datos, me encuentro con distintos valores para CADA variable:

Para este estudio canino, las variables cualitativas serán COLOR DEL PELO (blanco, miel, negro, gris...), FORMA DE LA CABEZA (mas larga que ancha, igual de larga que de ancha, intermedia entre las dos anteriores) y, las variables cuantitativas serán medidas numericamente: ALTURA (cm), PESO (Kg), LARGO DEL PELO (cm).

Una vez, encontrados los datos, estos deberán organizarse en una Base de Datos. Volviendo al ejemplo del chocolate, durante el estudio se organizaron los siguientes datos:

Persona Edad Sexo   Preferencia del chocolate

    1        18        M       Con leche

    2        21        M       Oscuro

    3        25        F        Blanco

    4        45        F        Con leche

    5        21        M       Con leche

Cada fila (horizontal) corresponderá a una sola observación -en el ejemplo hay 5 observaciones, que corresponden a 5 personas diferentes-.

Cada columna (vertical) es una variable - en el ejemplo hay 4 variables definidas: persona, edad, sexo, preferencia del chocolate-.

Niveles de medida de los datos

En las variables cualitativas, existen 3 niveles de medida: Nominal, Ordinal, Intervalos. Estos niveles nos determinarán cómo resumir y presentar la información en gráficas estadísticas y el tipo de análisis que se hará.

Variable Cualitativa Nominal Es el nivel más básico. Indica una categoría o cualidad como: sexo, color, religión, partido político, preferencia del chocolate. En este nivel no se requiere un orden específico para presentar la información. Los valores pueden estar representados bajo una palabra o un código numérico:   Para el caso de la variable sexo: Masculino (0), Femenino (1). Para el caso del color: azul (1), amarillo(2), verde(3), rojo(4)... Sin embargo, el hecho de que cada variable tenga designado un número, este no implica un orden específico, es simplemente un código. Para presentar el resumen de los datos generalmente se usa una FRECUENCIA o un PORCENTAJE. Por ejemplo: azul (1):       40% amarillo(2):  20%  verde(3):     10%  rojo(4):        50%

Variable Cualitativa Ordinal Este tipo de datos, generalmente se presenta en forma de rangos, niveles de satisfacción, o de deseos. Ejemplo:  1. La diferencia entre el primero y el segundo en llegar a la meta en una carrera de atletismo, puede ser muy pequeña, pero esta diferencia puede ser más grande frente a un tercer corredor: 1er corredor (1s) --2do corredor (2s) ------3er corredor (5s) 2. El grado de satisfacción por un servicio recibido puede tener grandes diferencias entre el nivel Satisfecho y el Insatisfecho y, muy poca diferencia entre Insatisfecho y Muy insatisfecho: Muy satisfecho - - Satisfecho - - - - - - Insatisfecho -Muy insatisfecho Tal como en las variables nominales, las variables ordinales, pueden presentarse con frecuencias: Nivel Frecuencia absoluta Frecuencia relativa (%) Desacuerdo (1) 7 35% Neutral (2) 4 20% ALgo de acuerdo (3) 3 15% Muy de acuerdo (4) 6 30% A este tipo de información nunca se le puede sacar un promedio.

Intervalos Este tipo de datos es más preciso y pueden ser más factible de ser ordenados, ya que son datos de tipo cuantitativos.  Ejemplo: número de clientes, peso, edad o talla. Los números en los datos cuantitativos, pueden ser números discretos (números enteros) o números continuos (números decimales). Discretos: 5 clientes 17 sedes 12 almacenes 24 puntos de venta Continuos:  La estatura dada en metros de un grupo de 4 personas en el intervalo (1.5 - 1.8]. 1.6 m 1.56 m 1.75 m 1.8 m El análisis de este tipo de datos es más versátil. Puede sacársele el promedio, la mediana o la desviación estándar

Variables Continuas Pueden tomar cualquier valor dentro de un rango en una escala definida. Por ejemplo: * El tiempo que toman los estudiantes en resolver el quiz de matemáticas: 1 hora 1.5 horas 0.5 horas 0.95 horas

Variables Discretas Este tipo de variables pueden tomar solo ciertos valores. Por ejemplo: * Número de niños con cabello castaño oscuro. * Cantidad de televisores vendidos. Los números son Enteros. No creo conveniente decir "le di pastel a un niño y medio" o "vendí 2 televisores y medio" 😉

Continúa estudiando DISTRIBUCIÓN DE FRECUENCIAS

Read More

Gráficas Estadísticas

GRÁFICAS ESTADÍSTICAS

¡Hola!

En esta ocasión, aprenderemos cómo representar graficamente los datos encontrados en una investigación estadística.

Generalmente, esto depende de los niveles de medida de los datos que hayamos escogido.

Los datos pueden ser presentados usando un diagrama circular, un diagrama de barras o un histograma. 

En la mayoría de los casos , para representar un solo conjunto de datos nominales se usa el diagrama de barras. Este tipo de datos no debe ser presentado en un diagrama circular.

Los datos cuantitativos en forma de rango, pueden ser representados en diagramas circulares, diagramas lineales o en histogramas.

Diagrama de Barras Una gráfica de barras es una gráfica que muestra los datos de la población clasificada en categorías, usando barras de diferentes alturas (una barra para cada categoría). Para hacerlo debe haberse organizando la información en una tabla de frecuencias. El diagrama de barras consta de dos ejes perpendiculares. El eje vertical representa la frecuencia absoluta y el eje horizontal las categorías en que se puede presentar la variable.  La longitud del eje vertical depende de los datos que se encuentren, por lo que se debe restar el mayor y el menor de los datos.  La longitud del eje horizontal depende de la cantidad de categorías. El espacio entre las barras debe ser igual al ancho de cada barra. Ejemplo Imagina que le haces una encuesta a tus amigos sobre su género de  películas favorito. Encuentras la siguiente información: Comedia:                4 Acción:                   5 Romance:               6 Drama:                   1 Ciencia Ficción:       4   Con un diagrama de barras, puedes graficar esta información de la siguiente forma: Fuente: Math is fun Este tipo de diagramas está bien usarlo si tus datos los has agrupado en categorías. En este caso tus categorías son los géneros de las películas: comedia, acción, romance drama y ciencia ficción.

Diagrama Circular Este diagrama es especial para mostrar el tamaño relativo de varias agrupaciones de datos, este tamaño relativo generalmente se presenta como porcentaje. Para hacerlo se debe tener a disposición, la tabla de distribución de frecuencias con las frecuencias relativas dadas en porcentaje. Para dibujar el diagrama, debes multiplicar cada frecuencia dada en porcentaje, por los 360° que tiene una circunferencia y usar el transportador.  GÉNERO DE PELÍCULA FAVORITA FRECUENCIA ABSOLUTA FRECUENCIA RELATIVA GRADOS COMEDIA 4 20% 72° ACCIÓN 5 25% 90° ROMANCE 6 30% 108° DRAMA 1 5% 18° CIENCIA FICCIÓN 4 20% 72° TOTAL 20 100% 360° Por ejemplo, si deseas presentar con un diagrama circular, la preferencia de películas de tus amigos, puedes elaborar la siguiente gráfica circular: Fuente: Math is fun Para iniciar el dibujo del diagrama, el 0° del transportador deberá coincidir con la parte superior del diagrama y así graficar la categoría COMEDIA. En seguida se rota el transportador y ahora el 0° del transportador va a conicidir con el límite inferior del sector que representa a las películas de comedia y se cuentan los grados de la siguiente categoría. En este caso la siguiente categoría corresponde a las películas de acción. Y así sucesivamente hasta terminar el diagrama circular.

Histograma En otras ocasiones, tus datos no pueden categorizarse y deben presentarse de forma continua, así que en lugar de categorías, presentas rangos, y graficas en lugar de un diagrama de barras, un Histograma, es decir, un diagrama que también usa barras, pero que no tiene espacio entre ellas y en el que debes indicar desde qué número hasta qué número va cada rango. Por ejemplo, si vas a graficar el precio de ciertos artículos, tu los puedes agrupar por rangos de precio, por ejemplo: de 100 a 150 pesos, de 150 a 200 pesos, de 200 a 250 pesos, etc. Así que en el eje vertical indicas la cantidad de artículos que hay en cada rango, pero en el eje horizontal, indicas el precio inicial y el precio final que forma el rango. Observa las diferencias entre un diagrama de barras y un histograma: Fuente: Math is fun Los histogramas son grandiosos para mostrar resultados de datos continuos, como: el peso, la estatura, el tiempo, etc. Para construir un histograma sigue los siguientes pasos: Paso 1. Ordena los datos.  Como ejemplo trabajaremos con la estatura de los estudiantes varones de un salón. Estos fueron los resultados: Estudiante Estatura (m) 1 1,56 2 1,58 3 1,54 4 1,63 5 1,58 6 1,76 7 1,63 8 1,78 9 1,67 10 1,65 11 1,63 12 1,83 13 1,54 14 1,57 15 1,64 16 1,71 17 1,56 18 1,55 19 1,45 20 1,54 21 1,55 22 1,71 Cantidad de datos : 22 Al terminar de recolectar la información, ordenamos los datos de menor a mayor y quedaron así: Estudiante Estatura (m) 19 1,45 3 1,54 13 1,54 20 1,54 18 1,55 21 1,55 1 1,56 17 1,56 14 1,57 2 1,58 5 1,58 4 1,63 7 1,63 11 1,63 15 1,64 10 1,65 9 1,67 16 1,71 22 1,71 6 1,76 8 1,78 12 1,83 Paso 2. Identifica el valor mínimo y el máximo. Mínimo: 1.45 Máximo: 1.83 Paso 3. Encuentra el rango. Resta el valor máximo y el mínimo ( para este caso encontramos la diferencia en centímetros: Rango= Máximo - Mínimo Rango= 183 - 145 = 38 Con el propósito de que en el primer intervalo quede el valor mínimo, adicionamos .1 al rango y encontramos un nuevo rango: Nuevo rango= 0.38 + 0.1 = 0.48 Paso 4. Elegir la cantidad de intervalos de clase.  Determina la cantidad de datos y encuentra su raíz cuadrada. Aproxima al entero más cercano. Cantidad de datos: 22 Raíz cuadrada de 22 = 4.69 4.69 aproximado al entero más cercano: 5 Paso 5. Encuentra la longitud o medida de cada intervalo de clase. Divide el rango entre el número de intervalos. 0.48 / 5 = 0.096  ≈ 0.1 0.1 será la medida que tendrá cada intervalo de clase. Paso 5. Definir los intervalos de clase. En este punto se recomienda construir una clase con los intervalos definidos y la frecuencia absoluta por cada intervalo. Intervalo Frecuencia Observa cómo definir los intervalos de clase con los datos de la estaturas. Iniciamos definiendo el primer intervalo y a partir de él, se definen los siguientes: Límite inferior del primer intervalo: Asignemos X como el valor mínimo del primer intervalo de clase. X = Mínimo - 0.05 X = 1.45 - 0.05 X = 1.4 Límite superior del primer intervalo: Límite inferior + longitud del intervalo. 1.4 + 0.1 = 1.5 y así sucesivamente, se suma la longitud del intervalo, hasta encontrar los límites de los 5 intervalos: Intervalo 1.4 - 1.5 1.5 - 1.6 1.6 - 1.7 1.7 - 1.8 1.8 - 1.9 Frecuencia Paso 6. Conteo de las frecuencias absolutas. En este paso, se debe contar las medidas que hay entre 1.4 y 1.5 m y registrar este valor en la tabla. Intervalo 1.4 - 1.5 1.5 - 1.6 1.6 - 1.7 1.7 - 1.8 1.8 - 1.9 Frecuencia 1 10 6 4 1 Esto indica por ejemplo, que para el primer intervalo de estaturas comprendido entre (1.4 - 1.5) solo hay un estudiante. En cambio para el intervalo siguiente, que comprende las estaturas entre (1.5 - 1.6) hay 10 estudiantes. Paso 7. Construye la Tabla de Frecuencias de Datos Agrupados Se toman las frecuencias absolutas (que es el número de estudiantes por cada intervalo de estaturas) y se trabaja como ya se sabe. INTERVALO FRECUENCIA ABSOLUTA FRECUENCIA RELATIVA FRACCIÓN DECIMAL PORCENTAJE 14-15 1 1/22 0.0454 4.54% 15-16 10 10/22 0.4545 45.45% 16-17 6 6/22 0.2727 27.27% 17-18 4 4/22 0.1818 18.18% 18-19 1 1/22 0.0454 4.54% total 22 1 1 100% Tabla de frecuencias de datos agrupados para las estaturas de los niños de un salón. En la tabla de frecuencias, se observa que el mayor porcentaje lo tiene el segundo intervalo (1.5 - 1.6 ), pero en la gráfica se aprecia con mayor facilidad que la mayoría de los estudiantes varones del salón mide entre 1.5 y 1.6 m y los intervalos de estaturas que le siguen en orden de mayor a menor por la altura de las barras.

Continúa aprendiendo Medidas de Tendencia Central

“AYÚDANOS A SALVAR EL PLANETA" 

TEN CONCIENCIA AMBIENTAL

PAPERLESS

Read More