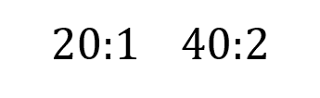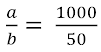ACTIVITY: Cookies
LEE CON ATENCIÓN Y COMPRENDE CÓMO SE RESOLVIO LA PROPORCIÓN.
LEE CON ATENCIÓN Y COMPRENDE CÓMO ENCONTRAR EL VALOR DE LA INCÓGNITA X.
COOKIES
Para hacer galletas, María agrega dos huevos por cada 300g de mantequilla. Si duplica la cantidad de mantequilla ¿cuántos huevos deberá usar?
Pistas:
Primero, determina cuál sería el antecedente y cuál el consecuente entre los huevos y la mantequilla.
Segundo, determina cuál es la incógnita.
Tercero, establece cómo quedaría la proporción.
Cuarto, resuelve usando la propiedad fundamental de las proporciones y encuentra el valor de la X. Usa la teoría que se te dió acerca de las proporciones.
ACTIVITY: Términos de las razones y proporciones
TÉRMINOS DE LAS RAZONES Y PROPORCIONES
Encuentra los términos solicitados por cada proporción. Observa los ejemplos.
ACTIVITY: Razones
RAZONES
Expresa los enunciados como una razón. Guíate con el ejemplo.
a.
Dos carros por
apartamento 2:1
b.
Cuatro naranjas por
cada seis peras ____
c.
Tres galletas por
cada dos panes ____
d.
Dos pantalones por
cada tres camisas ____
e.
Tres mujeres por cada
hombre ____
ACTIVITY: Mi abuela preferida - parte 2
source: www.freepik.com
¿CÓMO ES TU ABUELA PREFERIDA?
MI PREFERIDA:
Realiza el diagrama circular correspondiente de la composición de tu abuela preferida (Para saber el ángulo, multiplica 360° por el porcentaje y dibuja cada ángulo, con el transportador a partir de la línea que se te presenta a continuación)
ACTIVITY: Los amigos se van juntos
LOS AMIGOS SE VAN JUNTOS
Tres amigos están haciendo gimnasia en una plaza y tienen diferentes programas de entrenamiento. Uno da vueltas caminando, otro trotando y otro corriendo.
El primero tarda 10 minutos en dar una vuelta, el segundo tarda 6 minutos y el tercero 2 minutos.
PREGUNTAS
MARCA UNA SOLA RESPUESTA POR PREGUNTA.
Si reclamaste guía, rellena el óvalo correspondiente a la respuesta.Si respondes por classroom, responde el cuestionario.Si envías fotos de tu cuaderno, marca una X sobre la letra.
PARTE 1. Si comienzan a la misma hora y quieren saber si se pueden ir juntos a los 40 minutos:
A. Solo el que camina y el que corre podrán ir juntos. El que trota no podrá.
B. Solo el que camina y el que trota podrán ir juntos. El que corre no podrá.
C. Solo el que corre y el que trota podrán ir juntos. El que camina no podrá.
D. Ninguno puede.
PARTE 2. ¿a los cuántos minutos, podrán hacerlo? Encuentra el
MCM de los 3 números.
A.
A los 48 minutos
B.
A los 52 minutos
C.
A los 56 minutos
D. A los 60 minutos
ACTIVITY: Practiquemos deporte
PRACTIQUEMOS DEPORTE
MÍNIMO COMÚN MÚLTIPLO (repaso)
El mínimo común múltiplo de dos o más números es el menor múltiplo común
distinto de cero.
Así, que el primer múltiplo en común entre dos dígitos es llamado mínimo
común múltiplo y se abrevia como MCM.
En el caso de las plantas… al encontrar el primer múltiplo en común
encontramos el mínimo común múltiplo de 2 y 3: MCM(2,3)=6. Entonces a partir de
HOY, cada 6 días debo regar todas las plantas.
PREGUNTA
MARCA UNA SOLA RESPUESTA POR PREGUNTA.
Si reclamaste guía, rellena el óvalo correspondiente a la respuesta.Si respondes por classroom, responde el cuestionario.Si envías fotos de tu cuaderno, marca una X sobre la letra.
Mis compañeros Matías y Sandra coinciden en clase de Voleibol cada 2 y 5 días respectivamente. Si HOY practicaron juntos ese deporte ¿dentro de cuántos días volverán a coincidir?
A. 2
B. 5
C. 7
D. 10
ACTIVITY: Riego de la huerta
RIEGO DE LA HUERTA
Ahora, pensemos en nuestra huerta casera. Resulta que en la huerta de mi casa se tienen sembradas plantas que deben regarse cada 2 y 3 días y HOY me ha tocado regarlas todas.
Para resolver este problema primero encuentra los múltiplos de 2 y luego
los múltiplos de 3. Subraya los múltiplos comunes y señala la respuesta
correcta.
PREGUNTA
MARCA UNA SOLA RESPUESTA POR PREGUNTA.
Si reclamaste guía, rellena el óvalo correspondiente a la respuesta.Si respondes por classroom, responde el cuestionario.Si envías fotos de tu cuaderno, marca una X sobre la letra.
Para facilitar mi trabajo quiero saber dentro de cuántos días debo regarlas ambas otra vez:
A. 2
B. 3
C. 5
D. 6
ACTIVITY: Salchichas y panecillos
SALCHICHAS Y PANECILLOS
Ahora,
pensemos en perritos calientes o Hot Dogs. Imaginemos que vamos a hacer un “compartir”
en la escuela, y vamos a preparar perritos calientes. Pero hay un
inconveniente: los panecillos se venden en paquetes de 4 unidades y las
salchichas en paquetes de 6.
¿qué cantidad tenemos que comprar para que no sobren salchichas ni panecillos?
Para resolver esta situación, empecemos a hacer cuentas en nuestra mente
y buscamos un múltiplo del 4 y del 6 que den igual resultado:
Para las salchichas
Empecemos
multiplicando:
6
unid x 1 paq.= 6 salchichas
6
unid x 2 paq.= 12 salchichas
Para los panecillos:
4 unid x 1 paq.=4 panecillos
4 unid x 2 paq.=8 panecillos
4 unid x 3 paq.=12 panecillos
Y listo… resuelto el problema: Si compro 2 paquetes de salchichas, tendré 12 salchichas en total (2 paquetes x 6 salchichas/paquete = 12 salchichas)
Ahora, si compro 3 paquetes de panecillos, tendré 12 panecillos en total
(3 paquetes x 4 panecillos/paquete = 12)
Ahora me surgió otro problema: resulta que no somos 12 personas. Somos 48
en total.
PREGUNTA
MARCA UNA SOLA RESPUESTA POR PREGUNTA.
Si reclamaste guía, rellena el óvalo correspondiente a la respuesta.Si respondes por classroom, responde el cuestionario.Si envías fotos de tu cuaderno, marca una X sobre la letra.
¿Cuántos paquetes de salchichas y cuántos paquetes de panecillos se deben comprar para que nuestro compartir sea todo un éxito?
A. 2 paquetes de salchichas y 3 de panecillos.
B. 4 paquetes de salchichas y 6 de panecillos.
C. 6 paquetes de salchichas y 9 de panecillos.
D. 8 paquetes de salchichas y 12 de panecillos.
PROPORCIONES
PROPORCIONES
¡Hola!
Anteriormente vimos lo que significa una razón en matemáticas, ¿recuerdas?
Bueno, a partir de comprender lo que significa una razón nos será más fácil entender lo que significa una proporción.
Para comenzar, retomemos el ejemplo de las zanahorias y los tomates:
2:1
(La razón entre las zanahorias y los tomates es de 2 a 1, por cada dos zanahorias hay un tomate)
Luego, vimos la siguiente razón:
4:2
(La razón entre las zanahorias y los tomates es de 4 a 2, por cada cuatro zanahorias hay dos tomates)
Veíamos que las dos razones se relacionaban entre sí, pues la segunda razón se obtuvo de doblar las cantidades de zanahorias y tomates que forman la primera razón.
Con las proporciones podemos establecer una relación entre las dos razones, así:
1. Escribimos una razón frente a la otra.
2. Transformamos cada razón en fracción.
3. Escribimos un símbolo igual entre las fracciones.
4. Si al hacer la división que indica cada fracción, obtenemos igual resultado, podemos decir que hemos formado una proporción.
Validemos:
2/1 = 2
4/2 = 2
Con lo anterior podemos concluir que
UNA PROPORCIÓN ES UNA IGUALDAD ENTRE DOS O MÁS RAZONES.
Valida si las siguientes razones forman una proporción:
EJEMPLO:
La longitud y el peso de una soga son proporcionales. Cuando la soga mide 20m, pesa 1kg. Si añado 20m más, la soga pesará 2Kg
¿qué razones podemos establecer de la anterior información?
Podemos establecer dos razones:
¿las dos razones encontradas forman una proporción?
Esto quiere decir, que la longitud de la soga y su peso son magnitudes directamente proporcionales, pues cuando aumenta una, la otra también aumenta.
LAS PROPORCIONES SE USAN PARA ENCONTRAR EL VALOR DE UNA INCÓGNITA.
Encuentra la incógnita X y forma una proporción:
En los siguientes ejemplos, moveremos la incógnita de posición en la proporción planteada. Identifica cuáles son las esquinas y cuál sería el tercer número para resolver. Observa:
Ejemplo 1.
Ejemplo 2.
Resolvamos el siguiente problema, con la ayuda de lo aprendido. Ten en cuenta las recomendaciones que se te dan:
EL JUGO DE LUISA
RESUMEN:
Una proporción es una igualdad entre dos o más razones.
Se representa como una igualdad entre fracciones, así:
Se lee así: A es a B como C es a D.
Cada posición representada por cada letra tiene un nombre específico:
En la razón C/D, C es el antecedente y D es el consecuente.
En la proporción, A y D son los extremos.
En la proporción, B y C son los medios.
Cuando encontramos el resultado de dividir el antecedente entre el consecuente encontramos la constante de proporcionalidad.
En esta página, cada que validaste una proporción y viste a
es porque encontraste el cociente que forman las razones y validaste que eran iguales para ambas razones, lo cual te permitió establecer la constante de proporcionalidad para cada proporción trabajada.
Cuando encontramos el resultado de dividir el antecedente entre el consecuente encontramos la constante de proporcionalidad.
En esta página, cada que validaste una proporción y viste a
es porque encontraste el cociente que forman las razones y validaste que eran iguales para ambas razones, lo cual te permitió establecer la constante de proporcionalidad para cada proporción trabajada.PROPIEDADES DE LAS PROPORCIONES
Reflexiva
Todo elemento es igual a sí mismo.La razón 2:3 es igual a otra razón 2:3
Simétrica
Si un primer elemento está relacionado con un segundo elemento, entonces el segundo elemento está relacionado con el primero.La razón 1:4 está relacionada con la razón 2:8
Entonces, 2:8 está relacionada con 1:4
Reflexiva
Si una razón es equivalente a una segunda razón, y la segunda razón es equivalente a una tercera razón, entonces la primer razón es equivalente a la tercera razón.La razón 100:500 es equivalente a 10:50
y 10:50 es equivalente a 1/5
Entonces, 100:500 es equivalente a 1/5.
RAZONES
RAZONES
¡Hola!
En esta ocasión, hablaremos de lo que significa una razón en matemáticas:
UNA RAZÓN ES UNA COMPARACIÓN DE DOS VALORES Y me puede decir cuántas de unas cosas hay respecto de otras.
Entonces, una razón es
un número que resulta de comparar dos magnitudes a y b. (imagina que a es un número y b es
otro número).
Una razón se expresa de dos
formas:
* Como una división 
* ó de la forma a : b
Esta comparación se lee “a es a b”
Al término a la identificamos como el ANTECEDENTE
Y al término b lo identificamos como el CONSECUENTE
Ejemplo: ZANAHORIAS Y TOMATES
2:1
Hay 2 zanahorias y 1 tomate.
En una razón:
✓ Usa los dos puntos (:) para separar los valores. 2:1
✓ o puedes usar la partícula "a": 2 a 1
✓ o puedes escribirla como una fracción: 2/1
✓ También puedes usarla como escala:
4:2
Hay 4 zanahorias y 2 tomates.
En el ejemplo de las zanahorias y los tomates, si se divide a ambos lados de la razón, se observa que se mantiene la razón original 2 a 1, es decir que por cada dos zanahorias siempre hay un tomate.
Para usar una razón como una escala más pequeña, debes dividir ambos números de la razón.
Ejemplo 1:
En una receta de cupcakes, se usan 3 tazas de azúcar y dos tazas de leche para preparar 6 porciones.
La razón entre el azúcar y la leche es de 3:2 (3 a 2)
Si se desea preparar el doble de cupcakes, es decir 12 cupcakes, debemos multiplicar por 2 ambos números de la razón, con lo que obtenemos la nueva razón 6:4; si se desea preparar el triple, es decir 18 cupcakes, debemos multiplicar por 3 ambos números... observa la siguiente tabla:
Se puede comprobar que la razón se ha mantenido y que los cupcakes tendrán la misma consistencia de la receta original porque se ha mantenido la relación de cantidad entre el azúcar y la leche. Para validar esta información, lo único que debemos hacer es escribir las razones como fracciones y hacer las divisiones:
3/2 = 1.5
6/4 = 1.5
9/6 = 1.5
12/8 = 1.5
15/10 = 1.5
Ejemplo 2:
En una fiesta para 20 invitados se compró un pastel de 2 libras. Si se desean invitar 5 personas adicionales ¿qué cantidad de pastel se debe comprar ?
La razón entre el pastel y los invitados es de 2:20 (2 a 20)
Si se desea encontrar la relación entre el pastel y cinco invitados, debemos dividir cada número hasta que en el lado de los invitados obtengamos 5 ... observa la siguiente tabla:
Se puede comprobar que la razón entre pastel e invitados se ha mantenido y que a cada invitado adicional se le respetará su porción:
2/20 = 0.1
1/10 = 0.1
(0.5)/5 = 0.1
Ejemplo 3:
En una fies
Primero,
identificamos el antecedente y el consecuente:
a es la cantidad de estudiantes, es decir que a=1000 (antecedente)
b es la cantidad de profesores, es decir que b=50 (consecuente)
Segundo,
escribimos la razón como
y simplificamos hasta encontrar una fracción irreducible:
Tercero, reescribimos la razón con los valores resultantes:
Respuesta: Con esta información, podemos decir que hay 20 estudiantes por cada profesor. Una razón de 20 a 1 (20:1)
LAS RAZONES PUEDEN COMPARAR "PARTE CONTRA PARTE" O "PARTE CONTRA TODO"
Por ejemplo, si en un aula de clases, hay 32 estudiantes. De los cuales 18 son niños y 14 son niñas. Podemos establecer dos tipos de razones:
PARTE CONTRA PARTE
Razón entre niños y niñas: 18 a 14
simplificando: 9 a 7 (hay 9 niños por cada 7 niñas)
PARTE CONTRA TODO
Razón entre niños y el grupo: 18 a 32
simplificando 9 a 16 (hay 9 niños por cada 16 personas)
Razón entre niñas y el grupo: 14 a 32
simplificando 7 a 16 (hay 7 niñas por cada 16 personas)
OTRAS APLICACIONES DE LAS RAZONES:
En dibujo técnico, se utiliza mucho para dibujar a escala. Los arquitectos lo usan mucho para dibujar los planos de una casa o de un terreno. En estos casos, el primer número se refiere al dibujo en papel y el segundo número se refiere a la realidad del objeto.
En dibujo técnico, se utiliza mucho para dibujar a escala. Los arquitectos lo usan mucho para dibujar los planos de una casa o de un terreno. En estos casos, el primer número se refiere al dibujo en papel y el segundo número se refiere a la realidad del objeto.
Ejemplo: se desea dibujar un caballo que mide 1500 mm de alto y 2000 mm de largo. El dibujo que se realizó tiene una escala 1:10 (uno a diez). Las medidas resultantes en el papel fueron de 150 mm de alto y 200 mm de largo.
La escala 1:10 del ejemplo indica que por cada mm que se dibujó, debe multiplicarse por 10 para encontrar las dimensiones reales del caballo.
Entonces, para encontrar la altura real, se multiplicará 150mm x 10 y para encontrar el largo real, se multiplicará 200mm x 10
Suscribirse a:
Entradas (Atom)
Social Profiles
About me
- D_Gisela
- Ingeniera de Producción egresada de la Universidad Autónoma de Occidente, con experiencia y conocimientos en el área logística, manufactura, sistemas de información, normalización de procesos, mantenimiento de sistemas de gestión e implementación de proyectos de mejora en una organización. Soy una persona versátil, alegre, entusiasta... con aptitud para la escritura y disposición para trabajar en equipo.
Photos
Focus in Tit@