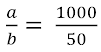RAZONES
¡Hola!
En esta ocasión, hablaremos de lo que significa una razón en matemáticas:
UNA RAZÓN ES UNA COMPARACIÓN DE DOS VALORES Y me puede decir cuántas de unas cosas hay respecto de otras.
Entonces, una razón es
un número que resulta de comparar dos magnitudes a y b. (imagina que a es un número y b es
otro número).
Una razón se expresa de dos
formas:
* Como una división 
* ó de la forma a : b
Esta comparación se lee “a es a b”
Al término a la identificamos como el ANTECEDENTE
Y al término b lo identificamos como el CONSECUENTE
Ejemplo: ZANAHORIAS Y TOMATES
2:1
Hay 2 zanahorias y 1 tomate.
En una razón:
✓ Usa los dos puntos (:) para separar los valores. 2:1
✓ o puedes usar la partícula "a": 2 a 1
✓ o puedes escribirla como una fracción: 2/1
✓ También puedes usarla como escala:
4:2
Hay 4 zanahorias y 2 tomates.
En el ejemplo de las zanahorias y los tomates, si se divide a ambos lados de la razón, se observa que se mantiene la razón original 2 a 1, es decir que por cada dos zanahorias siempre hay un tomate.
Para usar una razón como una escala más pequeña, debes dividir ambos números de la razón.
Ejemplo 1:
En una receta de cupcakes, se usan 3 tazas de azúcar y dos tazas de leche para preparar 6 porciones.
La razón entre el azúcar y la leche es de 3:2 (3 a 2)
Si se desea preparar el doble de cupcakes, es decir 12 cupcakes, debemos multiplicar por 2 ambos números de la razón, con lo que obtenemos la nueva razón 6:4; si se desea preparar el triple, es decir 18 cupcakes, debemos multiplicar por 3 ambos números... observa la siguiente tabla:
Se puede comprobar que la razón se ha mantenido y que los cupcakes tendrán la misma consistencia de la receta original porque se ha mantenido la relación de cantidad entre el azúcar y la leche. Para validar esta información, lo único que debemos hacer es escribir las razones como fracciones y hacer las divisiones:
3/2 = 1.5
6/4 = 1.5
9/6 = 1.5
12/8 = 1.5
15/10 = 1.5
Ejemplo 2:
En una fiesta para 20 invitados se compró un pastel de 2 libras. Si se desean invitar 5 personas adicionales ¿qué cantidad de pastel se debe comprar ?
La razón entre el pastel y los invitados es de 2:20 (2 a 20)
Si se desea encontrar la relación entre el pastel y cinco invitados, debemos dividir cada número hasta que en el lado de los invitados obtengamos 5 ... observa la siguiente tabla:
Se puede comprobar que la razón entre pastel e invitados se ha mantenido y que a cada invitado adicional se le respetará su porción:
2/20 = 0.1
1/10 = 0.1
(0.5)/5 = 0.1
Ejemplo 3:
En una fies
Primero,
identificamos el antecedente y el consecuente:
a es la cantidad de estudiantes, es decir que a=1000 (antecedente)
b es la cantidad de profesores, es decir que b=50 (consecuente)
Segundo,
escribimos la razón como
y simplificamos hasta encontrar una fracción irreducible:
Tercero, reescribimos la razón con los valores resultantes:
Respuesta: Con esta información, podemos decir que hay 20 estudiantes por cada profesor. Una razón de 20 a 1 (20:1)
LAS RAZONES PUEDEN COMPARAR "PARTE CONTRA PARTE" O "PARTE CONTRA TODO"
Por ejemplo, si en un aula de clases, hay 32 estudiantes. De los cuales 18 son niños y 14 son niñas. Podemos establecer dos tipos de razones:
PARTE CONTRA PARTE
Razón entre niños y niñas: 18 a 14
simplificando: 9 a 7 (hay 9 niños por cada 7 niñas)
PARTE CONTRA TODO
Razón entre niños y el grupo: 18 a 32
simplificando 9 a 16 (hay 9 niños por cada 16 personas)
Razón entre niñas y el grupo: 14 a 32
simplificando 7 a 16 (hay 7 niñas por cada 16 personas)
OTRAS APLICACIONES DE LAS RAZONES:
En dibujo técnico, se utiliza mucho para dibujar a escala. Los arquitectos lo usan mucho para dibujar los planos de una casa o de un terreno. En estos casos, el primer número se refiere al dibujo en papel y el segundo número se refiere a la realidad del objeto.
En dibujo técnico, se utiliza mucho para dibujar a escala. Los arquitectos lo usan mucho para dibujar los planos de una casa o de un terreno. En estos casos, el primer número se refiere al dibujo en papel y el segundo número se refiere a la realidad del objeto.
Ejemplo: se desea dibujar un caballo que mide 1500 mm de alto y 2000 mm de largo. El dibujo que se realizó tiene una escala 1:10 (uno a diez). Las medidas resultantes en el papel fueron de 150 mm de alto y 200 mm de largo.
La escala 1:10 del ejemplo indica que por cada mm que se dibujó, debe multiplicarse por 10 para encontrar las dimensiones reales del caballo.
Entonces, para encontrar la altura real, se multiplicará 150mm x 10 y para encontrar el largo real, se multiplicará 200mm x 10
