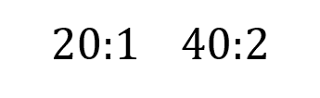PROPORCIONES
¡Hola!
Anteriormente vimos lo que significa una razón en matemáticas, ¿recuerdas?
Bueno, a partir de comprender lo que significa una razón nos será más fácil entender lo que significa una proporción.
Para comenzar, retomemos el ejemplo de las zanahorias y los tomates:
2:1
(La razón entre las zanahorias y los tomates es de 2 a 1, por cada dos zanahorias hay un tomate)
Luego, vimos la siguiente razón:
4:2
(La razón entre las zanahorias y los tomates es de 4 a 2, por cada cuatro zanahorias hay dos tomates)
Veíamos que las dos razones se relacionaban entre sí, pues la segunda razón se obtuvo de doblar las cantidades de zanahorias y tomates que forman la primera razón.
Con las proporciones podemos establecer una relación entre las dos razones, así:
1. Escribimos una razón frente a la otra.
2. Transformamos cada razón en fracción.
3. Escribimos un símbolo igual entre las fracciones.
4. Si al hacer la división que indica cada fracción, obtenemos igual resultado, podemos decir que hemos formado una proporción.
Validemos:
2/1 = 2
4/2 = 2
Con lo anterior podemos concluir que
UNA PROPORCIÓN ES UNA IGUALDAD ENTRE DOS O MÁS RAZONES.
Valida si las siguientes razones forman una proporción:
EJEMPLO:
La longitud y el peso de una soga son proporcionales. Cuando la soga mide 20m, pesa 1kg. Si añado 20m más, la soga pesará 2Kg
¿qué razones podemos establecer de la anterior información?
Podemos establecer dos razones:
¿las dos razones encontradas forman una proporción?
Esto quiere decir, que la longitud de la soga y su peso son magnitudes directamente proporcionales, pues cuando aumenta una, la otra también aumenta.
LAS PROPORCIONES SE USAN PARA ENCONTRAR EL VALOR DE UNA INCÓGNITA.
Encuentra la incógnita X y forma una proporción:
En los siguientes ejemplos, moveremos la incógnita de posición en la proporción planteada. Identifica cuáles son las esquinas y cuál sería el tercer número para resolver. Observa:
Ejemplo 1.
Ejemplo 2.
Resolvamos el siguiente problema, con la ayuda de lo aprendido. Ten en cuenta las recomendaciones que se te dan:
EL JUGO DE LUISA
RESUMEN:
Una proporción es una igualdad entre dos o más razones.
Se representa como una igualdad entre fracciones, así:
Se lee así: A es a B como C es a D.
Cada posición representada por cada letra tiene un nombre específico:
En la razón C/D, C es el antecedente y D es el consecuente.
En la proporción, A y D son los extremos.
En la proporción, B y C son los medios.
Cuando encontramos el resultado de dividir el antecedente entre el consecuente encontramos la constante de proporcionalidad.
En esta página, cada que validaste una proporción y viste a
es porque encontraste el cociente que forman las razones y validaste que eran iguales para ambas razones, lo cual te permitió establecer la constante de proporcionalidad para cada proporción trabajada.
Cuando encontramos el resultado de dividir el antecedente entre el consecuente encontramos la constante de proporcionalidad.
En esta página, cada que validaste una proporción y viste a
es porque encontraste el cociente que forman las razones y validaste que eran iguales para ambas razones, lo cual te permitió establecer la constante de proporcionalidad para cada proporción trabajada.PROPIEDADES DE LAS PROPORCIONES
Reflexiva
Todo elemento es igual a sí mismo.La razón 2:3 es igual a otra razón 2:3
Simétrica
Si un primer elemento está relacionado con un segundo elemento, entonces el segundo elemento está relacionado con el primero.La razón 1:4 está relacionada con la razón 2:8
Entonces, 2:8 está relacionada con 1:4
Reflexiva
Si una razón es equivalente a una segunda razón, y la segunda razón es equivalente a una tercera razón, entonces la primer razón es equivalente a la tercera razón.La razón 100:500 es equivalente a 10:50
y 10:50 es equivalente a 1/5
Entonces, 100:500 es equivalente a 1/5.
