¡Hola!
Te cuento que para que exista una función, debe haber una relación única entre el valor de entrada (los valores del eje X) y el valor de salida (los valores del eje Y). Entonces, todos los valores que tome X se convierten en el Dominio de la función y todos los valores que tomen Y, se convierten en el rango (conjunto solución).
💡 En este orden de ideas, TODA FUNCIÓN ES UNA RELACIÓN pero NO TODA RELACIÓN ES UNA FUNCIÓN.
EJEMPLOS:
1. Establezcamos una relación entre los modos de transporte (aéreo, acuático y terrestre) y los medios de transporte.
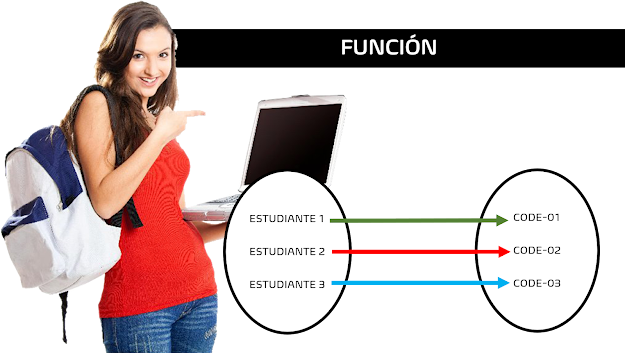
2. Establezcamos una relación-función entre los estudiantes y el código asignado en su institución educativa.
Veamos:
En este ejemplo, vemos como el modo de transporte se relaciona con varios medios de transporte. Esto es una RELACIÓN más no una FUNCIÓN.
En este ejemplo, vemos como a cada estudiante, le corresponde un sólo código. Esto es una RELACIÓN de tipo FUNCIÓN
Por otra parte, si se representan estos valores en el plano ordenado, se obtiene una serie de puntos (pares ordenados) que forman una línea recta o curva, la cual se llama gráfico de la función o gráfico de la ecuación Y = f ( X ) que representa la función. Como condición se tiene que, si después de graficada la ecuación y obtenida la línea recta o curva, se traza una línea vertical y esta corta en dos puntos diferentes la línea recta o curva graficada, pues la ecuación, no representaba una función, sino que representaba una relación. Entonces, es importante que tengas en cuenta que siempre haya para una X de entrada, una Y de salida.
Observa "EL COHETE QUE EXPLOTA":
Conoce, cómo calcular m (pendiente de la recta)
REPRESENTACIÓN EN EL PLANO COORDENADO:
Si tenemos una función de la forma Y=mX en donde, m es una constante, se tiene que para X=0, Y=0 lo que indica que la gráfica pasa por el origen o punto (0,0).
** recuerda que m es la pendiente.
En el ejemplo, la trayectoria del cohete que explota describe una línea recta, y m=1. Así que, reemplazando m en la función Y=mX tenemos:
Para X=0, Y=1*0 --> Y=0
Para X=1, Y=1*1 --> Y=1
para X=2, Y=1*2 --> Y=2
para X=3, Y=1*3 --> Y=3 y así sucesivamente.
¡PRACTICA Y APRENDE!
Para ampliar la información, visualiza los videos e intenta hacer los ejercicios en línea que se proponen luego:
Ejercicios On-line:
“AYÚDANOS A SALVAR EL PLANETA"
TEN CONCIENCIA AMBIENTAL
PAPERLESS
